Примеры Решения Задач Линейного Программирования

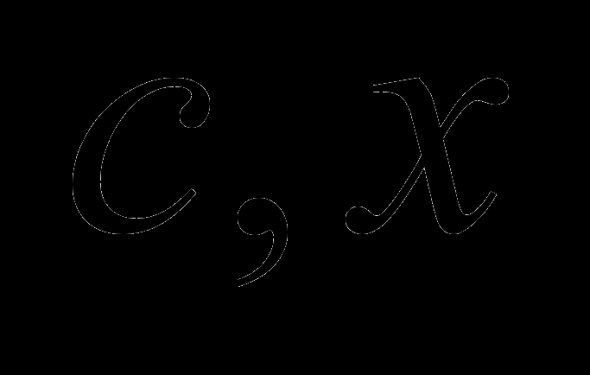
Симплекс-метод является универсальным методом, которым можно решить любую задачу линейного программирования. В отличие от симплекс-метода, графический метод пригоден для системы ограничений с двумя переменными.

Идея симплекс-метода состоит в следующем. Используя систему ограничений в виде системы m линейных уравнений с n переменными (m < n), находят её любое базисное решение, по возможности наиболее простое. Если первое же найденное базисное решение оказалось допустимым, то его проверяют на оптимальность. Если оно не оптимально, то переходят к другому допустимому базисному решению. Симплекс-метод гарантирует, что при этом новом решении линейная форма если и не достигнет оптимума (максимума или минимума), то приблизится к нему. С новым допустимым базисным решением поступают так же, пока не найдено решение, которое является оптимальным.

В отдельных статьях разобраны некоторые особые случаи: когда максимум целевой функции - бесконечность, когда система не имеет ни одного решения, и когда оптимальное решение - не единственное.

Далее разберём всё же типичный пример, когда система ограничений является совместной и имеется конечный оптимум, причём единственный.

Если первое найденное базисное решение окажется недопустимым, то с помощью симплекс-метода осуществляется переход к другим базисным решениям, которые позволяют приблизиться к области допустимых решений, пока на каком-то шаге не получится допустимое базисное решение. После этого к нему применяют механизм симплекс-метода, изложенный выше.

Таким образом, применение симплекс-метода распадается на два этапа:

1) нахождение допустимого базисного решения системы ограничений;

2) нахождение оптимального решения.

При этом каждый этап может включать несколько шагов, соответствующих тому или иному базисному решению. Так как число базисных решений всегда ограничено, то ограничено и число шагов симплекс-метода.

Всё более распространённой практикой, в том числе и для малого бизнеса, становится хранение всех данных, необходимых для рассчётов, в базе данных и вывод данных, необходимых для решения той или иной задачи, средствами программных приложений, использующих базы данных.

Пример. Найти максимум функции при ограничениях

Решение.

Шаг I (соответствует пунктам 1-3 ). Вводим добавочные неотрицательные переменные и сводим данную систему неравенств к эквивалентной ей системе уравнений

• Решение Задачи Линейного Программирования
• Транспортная Задача Линейного Программирования
• Двойственная Задача Линейного Программирования