Симплекс Метод Решения Задач Линейного Программирования
Симплексный метод решения задач линейного программирования
Июль 29, 2016 – 07:55
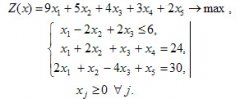
Симплексный метод
Данный метод является методом целенаправленного перебора опорных решений задачи линейного программирования. Он позволяет за конечное число шагов либо найти оптимальное решение, либо установить, что оптимальное решение отсутствует.
Основное содержание симплексного метода заключается в следующем:- Указать способ нахождения оптимального опорного решения
- Указать способ перехода от одного опорного решения к другому, на котором значение целевой функции будет ближе к оптимальному, т.е. указать способ улучшения опорного решения
- Задать критерии, которые позволяют своевременно прекратить перебор опорных решений на оптимальном решении или следать заключение об отсутствии оптимального решения.
Алгоритм симплексного метода решения задач линейного программирования
Для того, чтобы решить задачу симплексным методом необходимо выполнить следующее:- Привести задачу к каноническому виду
- Найти начальное опорное решение с "единичным базисом" (если опорное решение отсутствует, то задача не имеет решение ввиду несовместимости системы ограничений)
- Вычислить оценки разложений векторов по базису опорного решения и заполнить таблицу симплексного метода
- Если выполняется признак единственности оптимального решения, то решение задачи заканчивается
- Если выполняется условие существования множества оптимальных решений, то путем простого перебора находят все оптимальные решения
Пример решения задачи симплексным методом
Пример 26.1Решить симплексным методом задачу:
Решение:
Приводим задачу к каноническому виду.
Для этого в левую часть первого ограничения-неравенства вводим дополнительную переменную x6 с коэффициентом +1. В целевую функцию переменная x6 входит с коэффицентом ноль (т.е. не входит).
Получаем:
Находим начальное опорное решение. Для этого свободные (неразрешенные) переменные приравниваем к нулю х1 = х2 = х3 = 0.
Получаем опорное решение Х1 = (0, 0, 0, 24, 30, 6) с единичным базисом Б1 = (А4, А5, А6).
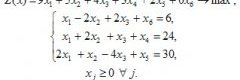
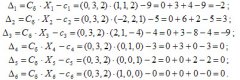
Source: www.grandars.ru
Похожие публикации