Геометрический Метод Решения Задач Линейного Программирования

Пример 6.1. Решить следующую задачу ли-нейного программирования геометрическим методом:

1 этап: построение прямых, ограничивающих область допустимых решений ( ОДР).

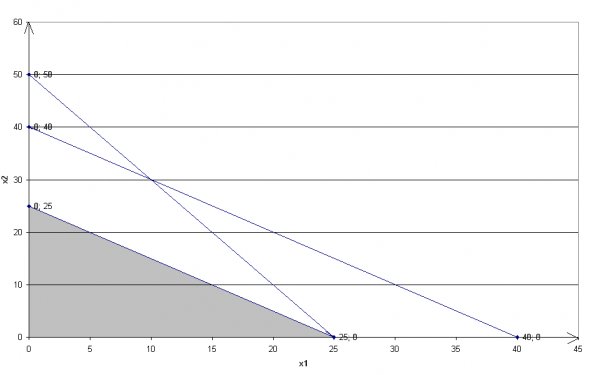
Рассмотрим систему ограничений задачи линейного програм-мирования (для удобства пронумеруем неравенства):

Рассмотрим первое ограничение, заменим знак неравенства знаком равенства и выразим переменную х2 через х1:

Аналогично определяем точки для остальных ограничений системы и строим по ним прямые, соответствующие каждому неравенству (рис. 1). Прямые пронумеруем согласно принятой ранее схеме.

2 этап: определение решения каждого из нера-венств системы ограничений.

Определим полуплоскости – решения каждого из неравенств.

Рассмотрим первое неравенство системы ограничений задачи. Возьмем какую-либо точку (контрольную точку), не принадлежащую соответствующей данному неравенству прямой, например, точку (0; 0). Подставим ее в рассматриваемое неравенство:

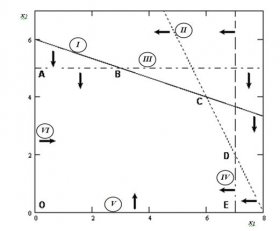
При подстановке координат контрольной точки неравенство остается справедливым. Следовательно, множество точек, принадлежащих данной прямой (т.к. неравенство не строгое), а также расположенных ниже ее, будут являться решениями рассматриваемого неравенства (пометим на графике (рис. 1) найденную полуплоскость двумя стрелками направленными вниз рядом с прямой ).

Аналогично определяем решения других неравенств и соответственно помечаем их графике. В результате график примет следующий вид:

3 этап: определение ОДР задачи линейного про- граммирования.

Найденные полуплоскости (решения каждого из неравенств системы ограничений) при пересечении образуют многоугольник ABCDEO, который и является ОДР рассматриваемой задачи.

Рис. 1. Область допустимых решений задачи

4 этап: построение вектора-градиента.

• Графический Метод Решения Задач Линейного Программирования Онлайн
• Симплекс Метод Решения Задач Линейного Программирования
• Симплексный Метод Решения Задач Линейного Программирования
• Графический Метод Решения Задачи Линейного Программирования
• Графический Метод Решения Задач Нелинейного Программирования